再來看一個簡單的線性迴歸的範例 (colab 筆記本在此)，以機器學習的方法，訓練一個一元一次方程式。

準備訓練資料

用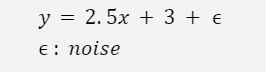

來生成所需的訓練資料。

Wtrue = 2.5
Btrue = 3
 
key = jrand.PRNGKey(7)
key, key1, key2 = jrand.split(key, num=3)
 
X = jrand.normal(key1, (100,))
Eps = jrand.normal(key2, (100,)) / 5.
Y = Wtrue * X + Btrue + Eps

畫出訓練資料的分布。

plt.scatter(X,Y)

output:

準備模型

在使用 JAX 時，一般來說，我們準備模型的步驟是這樣子的：

通常損失函式會參考到模型的定義，而參數調整方式會參考到損失函式。

# 線性迴歸模型
 
def linear_regression(theta, x):
    """
    theta = (w,b)
    """
    w, b = theta
    return w * x + b

# 損失函式
 
def loss_fn(theta, x, y):
    """
    theta = (w,b)
    """
    prediction = linear_regression(theta,x)
    return jnp.mean((prediction-y)**2)

# 參數調整
 
@jax.jit
def update(theta, x, y, lr=0.1):
    return theta - lr * jax.grad(loss_fn)(theta, x, y)

訓練模型

# theta 初值
theta = jnp.array([1., 1.])
 
# 訓練 epoch 迴圈
# =============================================================================================
#    將所有的訓練資料視為一個批次，一次輸入模型後調整一次參數
 
epochs = 1000
for _ in range(epochs):
    theta = update(theta, X, Y)
 
# 最終參數值
w, b = theta
print(f'W: {w:<.2f}, B: {b:<.2f}')

output:
W: 2.50, B: 3.00

模型相當精準的還原 W 和 B 的值。

plt.scatter(X, Y)
plt.plot(X, linear_regression(theta, X), color='brown')

output:

要注意的是，目前所舉的二個綜合演練的例子，它們都是將整個訓練資料視為單一批次而進行訓練，而模型設定本身，就能夠一次接受所有的資料，因此還沒有用到批次及 vmap 相關的功能。稍後，當老頭要介紹比較複雜的模型時，再來舉例說明。